总结: 随着我们增加内存压缩次数的次数,Infini-attention 的性能会变得越来越差。据我们所知,ring attention、YaRN 和 rope scaling 这三种方法仍是将预训练模型拓展更长上下文的最佳方式。
引言:
语言模型的上下文长度也是除模型性能之外的重要属性之一。自 in-context learning (上下文学习) 出现以来,添加相关信息到模型的输入中日渐重要。因此,上下文长度迅速从段落 (BERT/GPT-1 的 512 个 tokens) 扩展到页面 (GPT-2 和 GPT-3 分别为 1024/2048 个 tokens), 再到书籍 (Claude 的 128k tokens), 甚至书籍集合 (Gemini 的 1-10M tokens)。然而,将 standard attention(标准注意力) 扩展到如此长度仍然面临挑战。
关于 Ring Attention (一种注意力机制) 的简单介绍: 据我们所知,Ring Attention 最初是由加州大学伯克利分校的研究人员在 2024 年提到的 Ring Attention with Blockwise Transformers for Near-Infinite Context。这种工程技术通过以分块方式执行 self-attention 和 feedforward network 计算,并将序列维度分配到多个设备上,减轻了内存限制,实现并发计算和通信。
即使使用 Ring Attention,要在 1 百万 token 的上下文长度上训练一个 Llama 3 8B 模型,batch size 为 1 时,仍然需要 512 个 GPU。正如 scaling laws (扩展定律) 提到 Scaling Laws for Neural Language Models 的那样,模型大小与其下游任务性能之间存在强相关性,这意味着模型越大越好 (当然,两种模型都应该被训练得很好)。因此,我们不仅需要 1 百万 token 的上下文长度,还希望在最大的模型上实现这一长度 (例如,Llama 3 8B 405B)。而目前只有少数几家公司拥有实现这一目标的资源。
回顾自注意力的内存复杂度
在标准注意力机制 (非 flash-attention) 中,每个标记都会关注序列中的所有其他标记,从而形成一个大小为 [seq_len, seq_len] 的注意力矩阵。对于每对标记,我们都需要计算一个注意力分数。随着序列长度 (seq_len) 的增加,内存和计算需求呈二次方增长:注意力矩阵的内存复杂度为 O(seq_len^2)。例如,序列长度增加 10 倍会导致内存需求增加 100 倍。
即使是像 Flash Attention 这样的内存高效注意力方法,其内存需求仍会随上下文长度线性增长,并受限于单个 GPU 的内存容量。这导致在当今的 GPU 上,典型的最大上下文长度远低于 1M 个标记。
受此启发,我们探索了一种替代标准注意力的方法:无限注意力 (infini-attention)。这篇论文由来自 Google 的研究人员于 2024 年 4 月发布 Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention。与计算每个词之间的注意力分数不同,无限注意力将序列划分为多个片段,将早期片段压缩到固定缓冲区,并允许下一个片段从早期片段中检索记忆,同时将注意力分数限制在当前片段内的词语之间。其关键优势在于固定的缓冲区大小为总内存使用设置了上限。它还在一个片段内使用相同的查询来访问该片段和压缩记忆中的信息,这使我们能够以低成本为预训练模型扩展上下文长度。理论上,我们可以实现无限长的上下文,因为它只为所有早期片段的记忆保留一个缓冲区。然而,实际上压缩限制了能有效存储的信息量,因此问题在于:这种压缩的记忆有多大的可用性 ?
虽然在理论上理解新方法相对容易,但实际使其运作往往是另一回事,而这个过程很少公开分享。出于这个原因,我们决定分享我们在复现无限注意力论文过程中的实验和记录,包括在调试过程中 (我们 90% 的时间都在调试一个收敛问题) 激励我们的因素,以及让这些方法正常工作可能有多困难。
随着 Llama 3 8B (上下文长度限制为 8k 个标记) 的发布,我们试图将这个长度扩展到 100 万个标记,而不会导致内存需求二次增长。在这篇博客中,我们将首先解释无限注意力的工作原理。然后,我们将介绍我们的复现原则,并描述我们最初的小规模实验。我们讨论了面临的挑战,如何解决这些挑战,并以我们的发现总结和其他探索的想法作为结束。如果你有兴趣测试我们训练的 检查点, 你可以在 以下仓库 中找到它 (请注意,我们目前按原样提供代码)。
第 1 节: 复现原则
我们发现以下规则在实现新方法时很有帮助,并将其用作我们大量工作的指导原则:
- 原则 1: 从能提供良好信号的最小模型规模开始,一旦获得良好信号就扩大实验规模。
- 原则 2: 始终训练一个可靠的基准模型来衡量进展。
- 原则 3: 为了确定某项修改是否提高了性能,训练两个除了被测试的修改之外完全相同的模型。
牢记这些原则,让我们深入了解 Infini-attention 的实际工作原理。理解其机制对于我们推进实验至关重要。
第 2 节: Infini-attention 的工作原理
- 步骤 1: 将输入序列分割成较小的、固定大小的块,称为 “ 片段 “。
- 步骤 2: 在每个片段内计算标准的因果点积注意力。
-
步骤 3: 使用当前片段的查询向量从压缩内存中提取相关信息。检索过程的数学定义如下:
$ A{\text {mem }}=\frac{\sigma(Q) M{s-1}}{\sigma(Q) z_{s-1}} $
- $ A{\text {mem }} \in \mathbb{R}^{N \times d{\text {value }}} $ : 从内存中检索的内容,表示长期上下文。
- $ Q \in \mathbb{R}^{N \times d{\text {key }}} $ : 查询矩阵,其中 $ N $ 是查询的数量,$ d{\text {key }} $ 是每个查询的维度。
- $ M{s-1} \in \mathbb{R}^{d{\text {key }} \times d_{\text {value }}} $ : 来自前一个片段的内存矩阵,存储键值对。
- $ \sigma $: 非线性激活函数,具体为逐元素指数线性单元 (ELU) 加 1。
- $ z{s-1} \in \mathbb{R}^{d{\text {key }}} $ : 归一化项。
import torch.nn.functional as F
from torch import einsum
from einops import rearrange
def _retrieve_from_memory(query_states, prev_memory, prev_normalization):
...
sigma_query_states = F.elu(query_states) + 1
retrieved_memory = einsum(
sigma_query_states,
prev_memory,
"batch_size n_heads seq_len d_k, batch_size n_heads d_k d_v -> batch_size n_heads seq_len d_v",
)
denominator = einsum(
sigma_query_states,
prev_normalization,
"batch_size n_heads seq_len d_head, batch_size n_heads d_head -> batch_size n_heads seq_len",
)
denominator = rearrange(
denominator,
"batch_size n_heads seq_len -> batch_size n_heads seq_len 1",
)
# NOTE: because normalization is the sum of all the keys, so each word should have the same normalization
retrieved_memory = retrieved_memory / denominator
return retrieved_memory-
步骤 4: 将局部上下文 (来自当前片段) 与长期上下文 (从压缩内存中检索) 结合,生成最终输出。这样,注意力输出可以同时考虑短期和长期上下文。
$ A=\text{sigmoid}(\beta) \odot A{\text {mem }}+(1-\text{sigmoid}(\beta)) \odot A{\text {dot }} $
- $ A \in \mathbb{R}^{N \times d_{\text {value }}} $ : 组合后的注意力输出。
- $ \text{sigmoid}(\beta) $ : 一个可学习的标量参数,用于控制长期内存内容 $ A_{\text {mem }} $ 和局部上下文之间的权衡。
- $ A{\text {dot }} \in \mathbb{R}^{N \times d{\text {value }}} $ : 使用点积注意力从当前片段得到的注意力输出。
-
步骤 5: 通过添加当前片段的键值状态来更新压缩内存,这使我们能够随时间累积上下文。
$ Ms \leftarrow M{s-1}+\sigma(K)^T V $
$ zs \leftarrow z{s-1}+\sum_{t=1}^N \sigma\left(K_t\right) $
- $ Ms \in \mathbb{R}^{d{\text {key }} \times d_{\text {value }}} $ : 当前片段的更新后内存矩阵,包含了新信息。
- $ K \in \mathbb{R}^{N \times d_{\text {key }}} $ : 当前片段的键矩阵,表示要存储的新键。
- $ V \in \mathbb{R}^{N \times d_{\text {value }}} $ : 当前片段的值矩阵,表示与键相关联的新值。
- $ K_t $ : 键矩阵中的第 $ t $ 个键向量。
- $ z_s $ : 当前片段更新后的归一化项。
import torch
def _update_memory(prev_memory, prev_normalization, key_states, value_states):
...
sigma_key_states = F.elu(key_states) + 1
if prev_memory is None or prev_normalization is None:
new_value_states = value_states
else:
numerator = einsum(
sigma_key_states,
prev_memory,
"batch_size n_heads seq_len d_k, batch_size n_heads d_k d_v -> batch_size n_heads seq_len d_v",
)
denominator = einsum(
sigma_key_states,
prev_normalization,
"batch_size n_heads seq_len d_k, batch_size n_heads d_k -> batch_size n_heads seq_len",
)
denominator = rearrange(
denominator,
"batch_size n_heads seq_len -> batch_size n_heads seq_len 1",
)
prev_v = numerator / denominator
new_value_states = value_states - prev_v
memory = torch.matmul(sigma_key_states.transpose(-2, -1), new_value_states)
normalization = reduce(
sigma_key_states,
"batch_size n_heads seq_len d_head -> batch_size n_heads d_head",
reduction="sum",
...
)
memory += prev_memory if prev_memory is not None else 0
normalization += prev_normalization if prev_normalization is not None else 0
return memory, normalization- 步骤 6: 当我们从一个片段移动到下一个片段时,我们丢弃前一个片段的注意力状态,并将更新后的压缩内存传递给下一个片段。
def forward(...):
...
outputs = []
global_weights = F.sigmoid(self.balance_factors)
...
local_weights = 1 - global_weights
memory = None
normalization = None
for segment_hidden_state, segment_sequence_mask in zip(segment_hidden_states, segment_sequence_masks):
attn_outputs = self.forward_with_hidden_states(
hidden_states=segment_hidden_state, sequence_mask=segment_sequence_mask, return_qkv_states=True
)
local_attn_outputs = attn_outputs["attention_output"]
query_states, key_states, value_states = attn_outputs["qkv_states_without_pe"]
q_bs = query_states.shape[0]
q_length = query_states.shape[2]
...
retrieved_memory = _retrieve_from_memory(
query_states, prev_memory=memory, prev_normalization=normalization
)
attention_output = global_weights * retrieved_memory + local_weights * local_attn_outputs
...
output = o_proj(attention_output)
memory, normalization = _update_memory(memory, normalization, key_states, value_states)
outputs.append(output)
outputs = torch.cat(outputs, dim=1) # concat along sequence dimension
...既然我们已经掌握了理论,现在该动手进行一些实际实验了。我们先从小规模开始,以便快速获得反馈并迅速迭代。
第 3 节: 小规模的首次实验
Llama 3 8B 模型相当大,所以我们决定从 200M 的 Llama 开始,使用 Nanotron 和 Fineweb 数据集 从头预训练 Infini-attention。一旦我们在 200M 模型上获得了良好的结果,我们就继续对 Llama 3 8B 进行持续预训练。
我们使用了 200 万个 token 的 batch size,256 的上下文长度,1 的梯度裁剪,0.1 的权重衰减,前 5000 次迭代是线性预热,而剩余的步骤是余弦衰减,学习率为 3e-5。
使用密钥检索任务进行评估
密钥检索任务最初由 EPFL 的研究人员提出 Landmark Attention: Random-Access Infinite Context Length for Transformers。这是一个旨在评估模型从长上下文中检索信息的能力的任务,其中信息的位置是可控的。提示模型的输入格式结构如下:
在大量无关文本中隐藏着重要信息。找到并记住它们。我将就其中的重要信息对你进行测试。草是绿色的。天空是蓝色的。太阳是黄色的。我们开始吧。来回往复。(重复 x 次) 密钥是 9054。记住它。9054 是密钥。草是绿色的。天空是蓝色的。太阳是黄色的。我们开始吧。来回往复。(重复 y 次) 密钥是什么?密钥是我们认为,如果模型的输出包含 “信息点” (在上述例子中为 “9054”),则模型在此任务中成功,否则失败。在实验中,我们将 “信息点” 放置在上下文的不同位置,具体为总上下文长度的 0%、5%、10%、…、95% 和 100% 处 (0% 为距离生成标记最远的位置)。例如,如果上下文长度为 1024 个 token,将 “信息点” 放在 10% 处意味着它位于约第 102 个 token 处。对于每个深度位置,我们使用 10 个不同的样本测试模型并计算平均成功率。
首次结果
这里是在小型 200M 模型上的一些首次结果:

如你所见,这在某种程度上是有效的。观察样本生成可以发现,Infini-attention 生成的内容与先前段落相关。
Infini-attention 通过以第一段的全部内容为条件来预测第二段的第一个 token,生成的第一个 token 是 “_grad”,这提供了一个良好的信号。为验证这个信号是否为假阳性,我们假设 Infini-attention 生成与先前段落相关的内容是因为当给定 “_grad” 作为第二段的第一个生成 token 时,它总是生成 PyTorch 相关的教程,而这恰好与先前段落相关。因此,我们进行了一个健全性测试,唯一的输入 token 是 “_grad”,它生成了下列结果。这表明它确实使用了记忆,但使用得不够好 (无法检索到确切的 needle 或继续先前段落的确切内容)。
_graduate_education.html
Graduate Education
The Department of Physics and Astronomy offers a program leading to the Master of Science degree in physics. The program is designed to provide students with a broad background in基于这些结果,模型似乎确实使用了压缩内存。我们决定通过持续预训练 Llama 3 8B 来扩大实验规模。不幸的是,当 needle 位于较早的段落时,模型未能通过 needle 评估。
我们检查了所有层的平衡因子 (用于平衡压缩和非压缩内存量的因子)。图 3a 和图 3b 显示,约 95% 的权重集中在 0.5 左右。回想一下,权重收敛到理想范围取决于两个一般因素: 步长和梯度幅度。但 Adam 将梯度归一化到幅度 1,因此问题变为: 训练超参数是否正确,能使微调收敛?
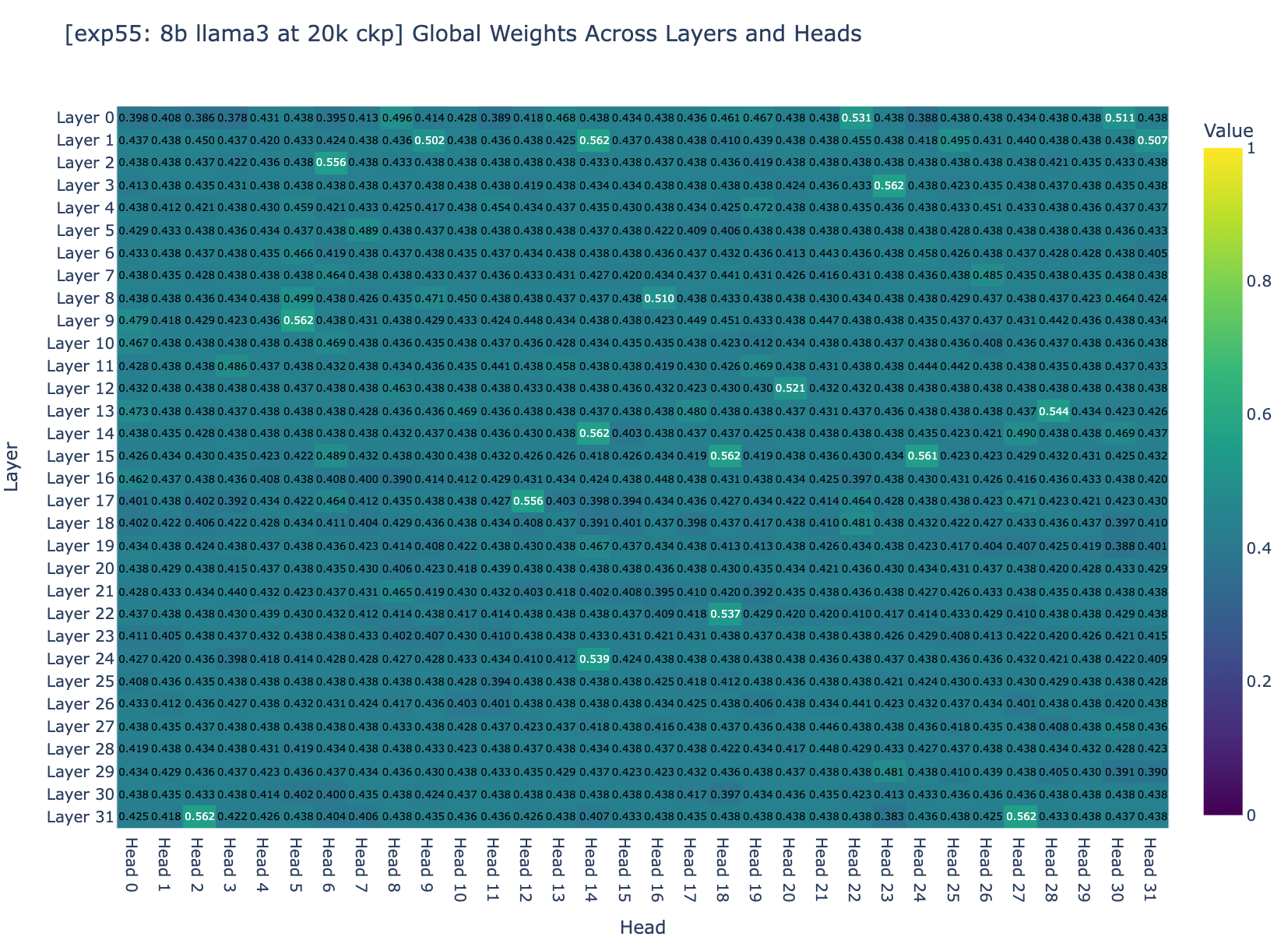
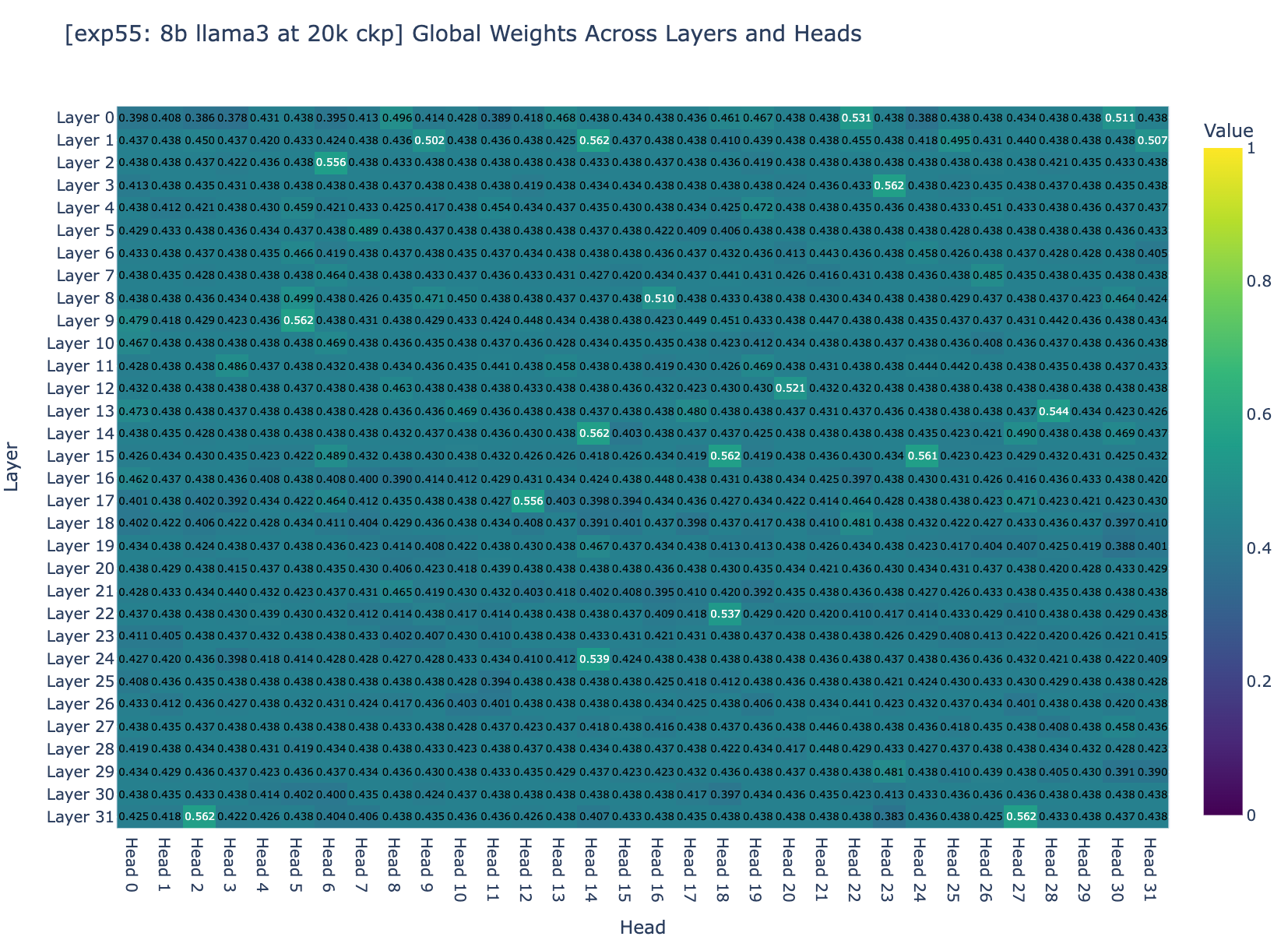
第 4 节: 研究收敛性?
我们决定模拟训练期间平衡权重的变化,假设梯度在良好范围内 (L2 范数为 0.01)。根据最后一次 8B LLaMA3 微调实验的配置,权重的绝对变化总和为 0.03。平衡因子初始化为 0 (在这种情况下无关紧要),最终权重范围在 [-0.03, 0.03] 之间。
我们推测,无限注意力在全局权重分布于 0 到 1 之间时效果最佳,如论文中所述。给定上述权重,sigmoid([-0.03, 0.03]) = tensor([0.4992, 0.5008]),这与我们之前平衡因子约为 0.5 的实验结果一致。接下来,我们计划对平衡因子使用更高的学习率 (其他所有参数使用 Llama 3 8B 的学习率),并增加训练步骤数,使平衡因子至少变化 4,以便在梯度下降需要时,全局权重能达到理想值 (sigmoid(-4) ≈ 0,sigmoid(4) ≈ 1)。
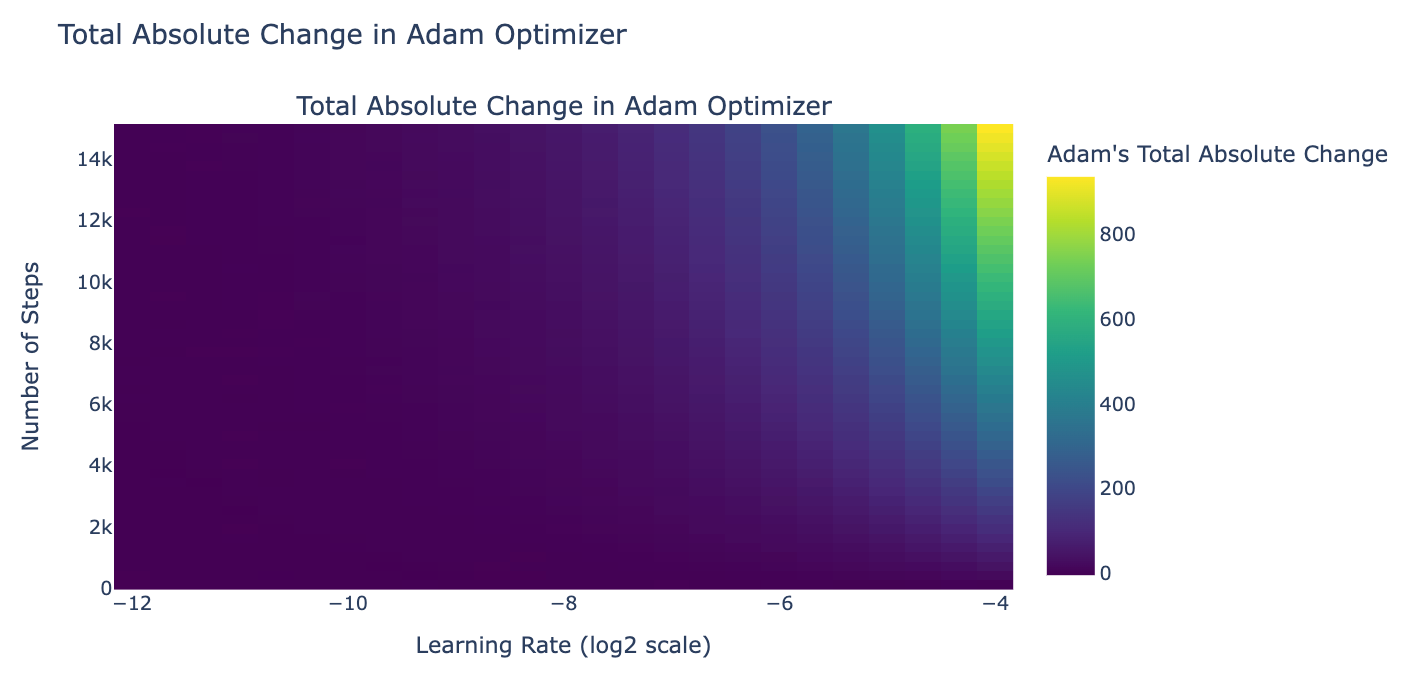
我们还注意到,由于梯度并不总是朝同一方向,会发生抵消现象。这意味着我们应该目标设定为显著大于总绝对变化的学习率和训练步骤。回想一下,Llama 3 8B 的学习率是 3.0×10^-4,这意味着如果我们将其用作全局学习率,门控将无法以任何方式收敛。
结论: 我们决定采用 3.0×10^-4 的全局学习率和 0.01 的门控学习率,这应该能使门控函数收敛。
使用这些超参数,无限注意力 (Infini-attention) 中的平衡因子变得可训练,但我们观察到 200M llama 的损失在 20B 标记后变为 NaN (我们尝试了从 0.001 到 1.0e-6 的学习率)。我们在 20B 标记检查点 (10k 训练步骤) 处调查了一些生成结果,您可以在图 4a 中看到。模型现在能够继续精确的内容并回忆身份信息 (如果记忆被移除,它会生成垃圾内容)。
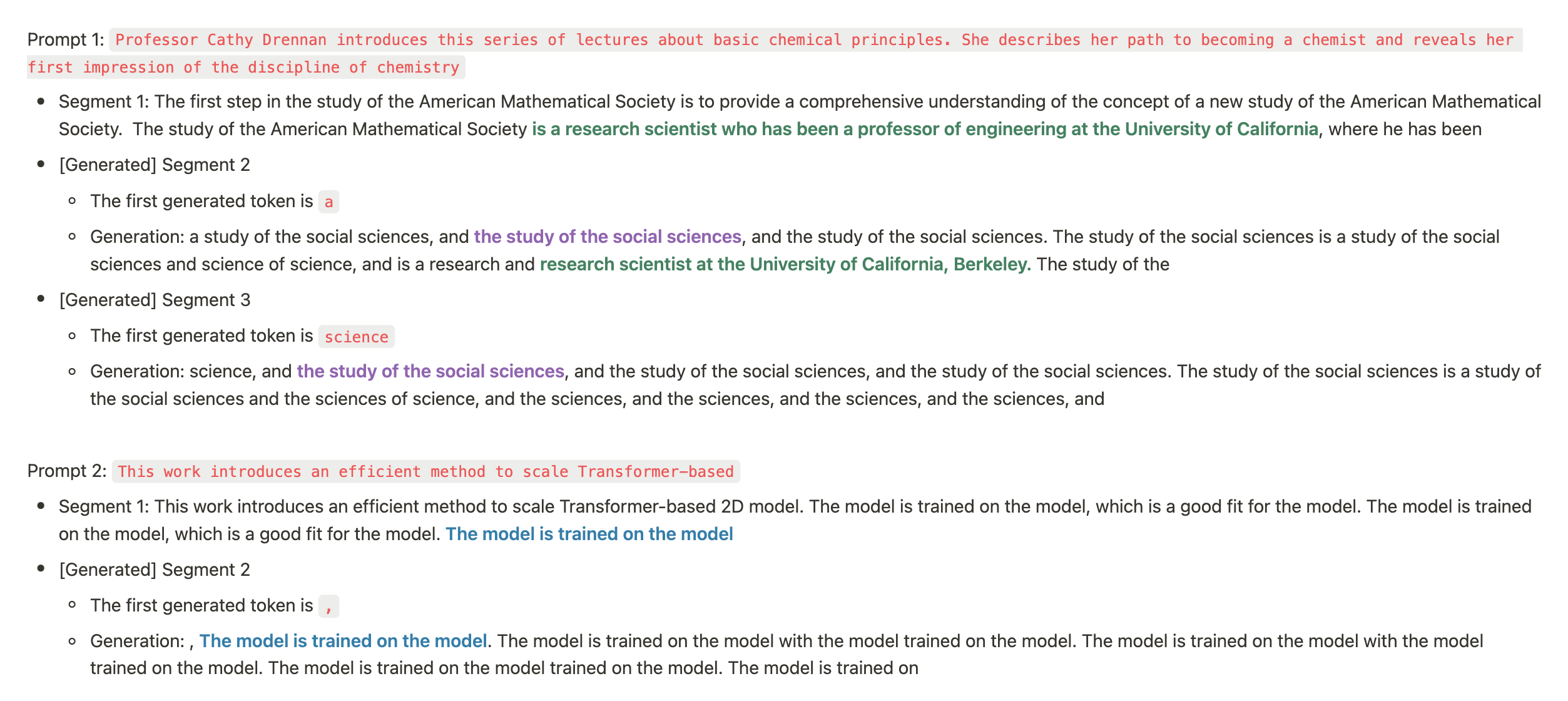
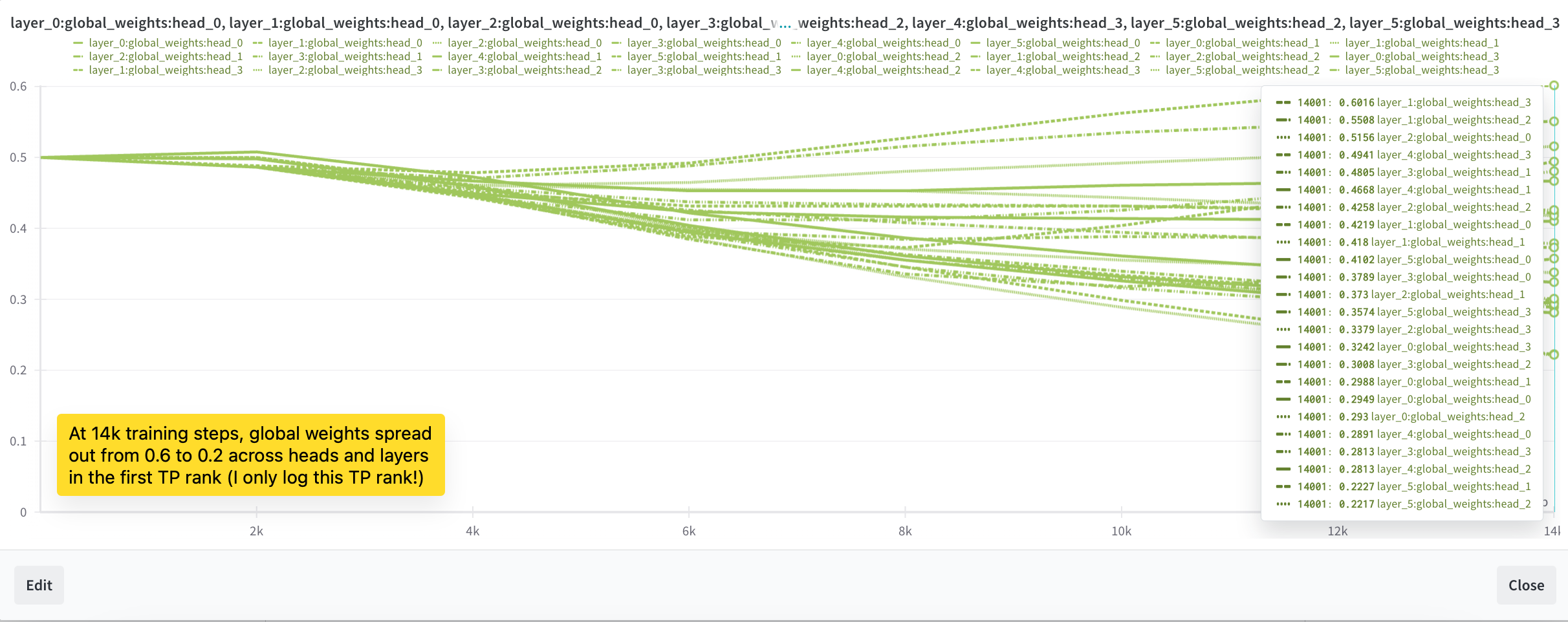
但模型仍无法在不同段落间检索信息点 (在同一段落内能可靠完成)。当信息点位于第一段时,信息点评估完全失败 (位于第二段时 100% 成功,共 2 段)。如图 4b 所示,我们还观察到平衡因子在 5,000 步后停止变化。尽管有所进展,我们还未完全解决问题。平衡因子的表现仍不如预期。我们决定进一步深入研究并做出更多调整。
第五节: 平衡因子无权重衰减
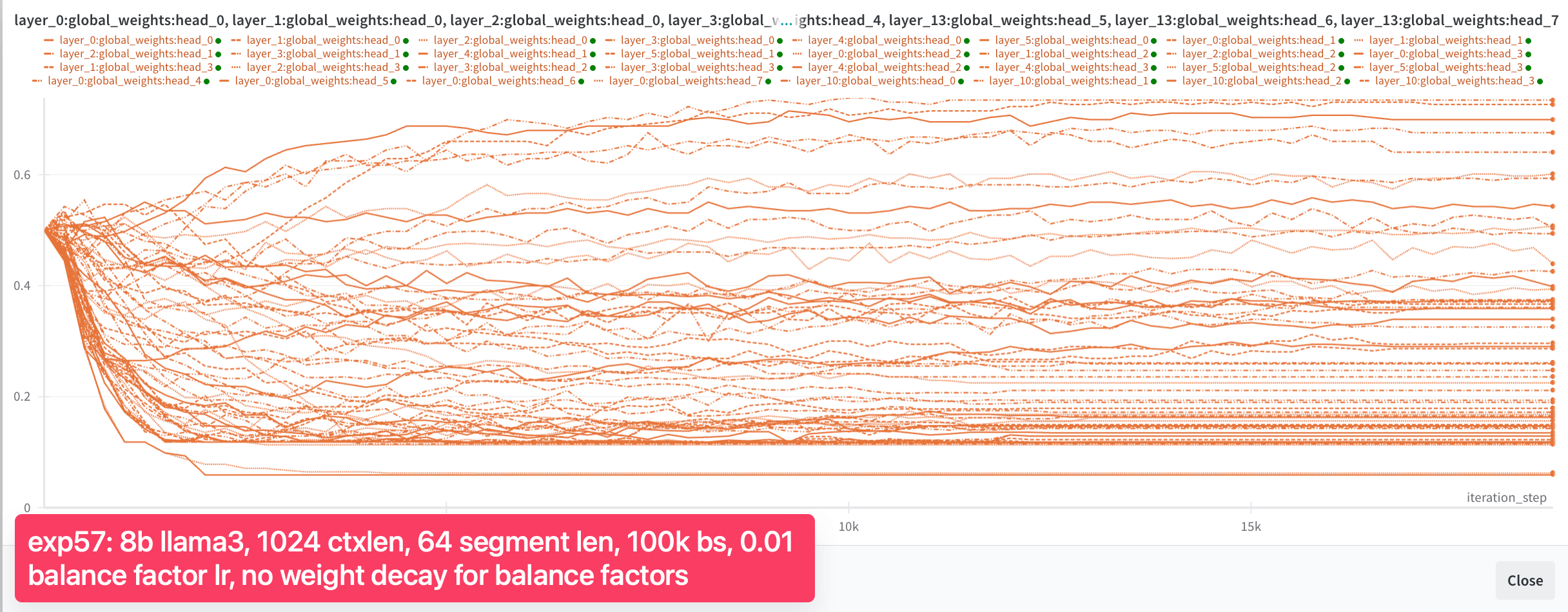
再次详细检查平衡因子,我们看到了一些进展: 现在约 95% 的头显示全局权重在 0.4 到 0.5 之间,没有头的全局权重大于 0.6。但权重仍然不在理想范围内。
我们想到了另一个可能的原因: 权重衰减,它鼓励平衡因子的 L2 范数较小,导致 sigmoid 值收敛接近零,因子集中在 0.5 左右。
另一个可能的原因是我们使用的展开太小。在 200m 实验中,我们只使用了 4 次展开,在 8b 实验中,我们只使用了 2 次展开 (8192**2)。使用更大的展开应该能激励模型压缩并更好地利用内存。因此,我们决定将展开次数增加到 16,并且不使用权重衰减。我们将上下文长度缩小到 1024,使用 16 次展开,得到 64 的段长度。
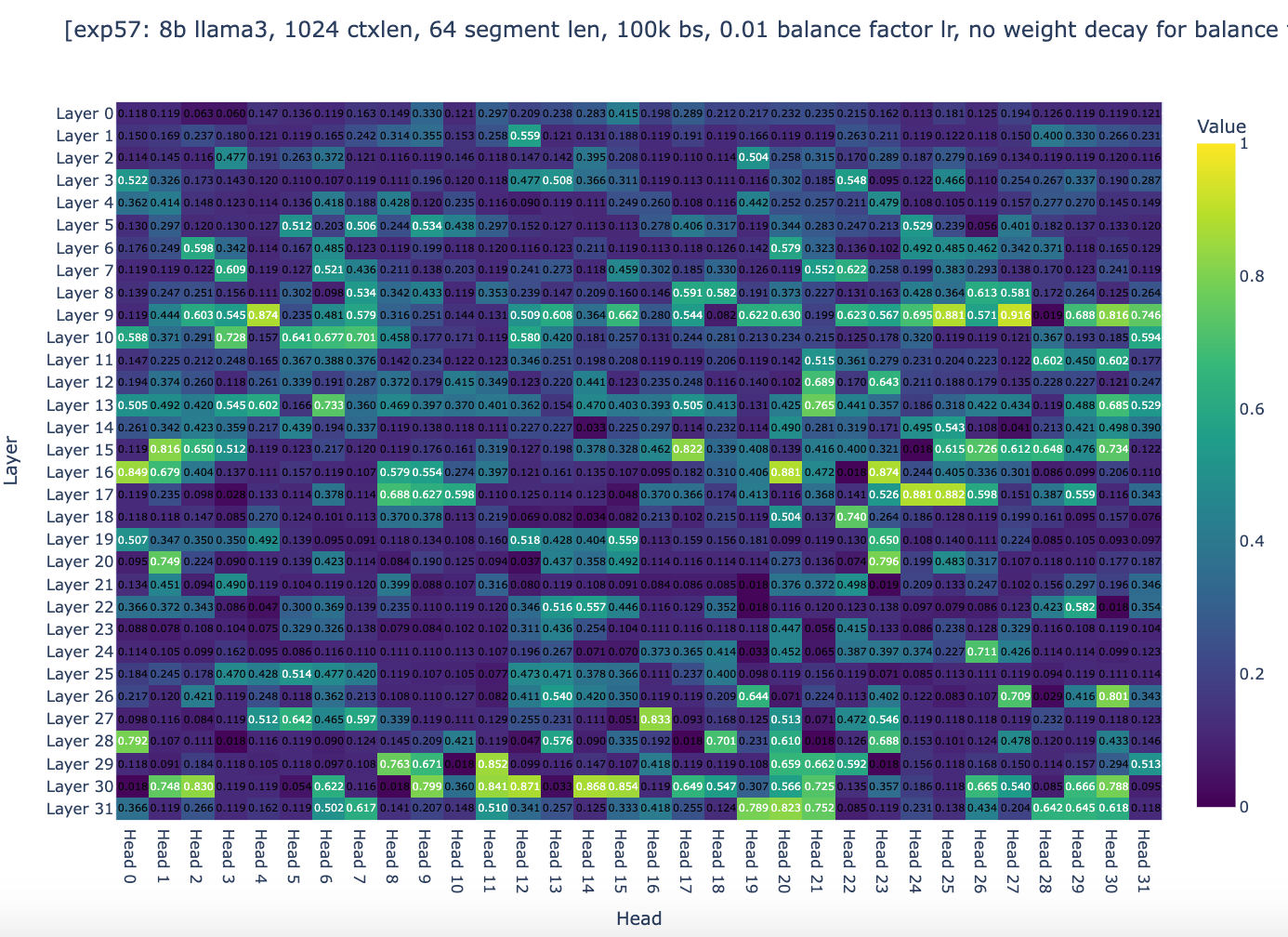
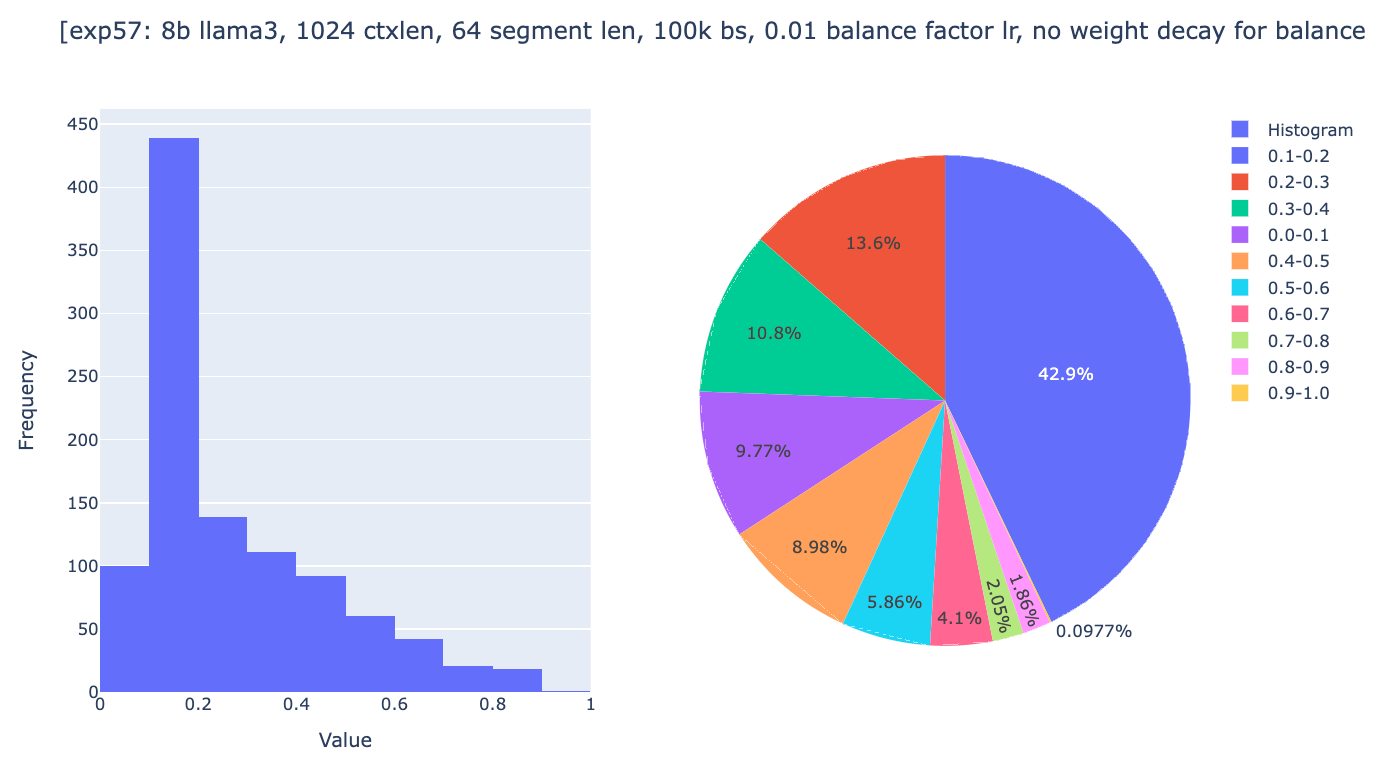
如你所见,全局权重现在分布在 0 到 1 的范围内,其中 10% 的注意力头的全局权重在 0.9 到 1.0 之间,尽管在 18k 步之后,大多数注意力头停止了全局权重的变化。然后,我们相当有信心,如果梯度下降的精神与我们同在,这些实验的设置将允许收敛。唯一剩下的问题是 Infini-attention 的一般方法是否能够足够好地工作。
以下评估是在 1.5B 词元上运行的。

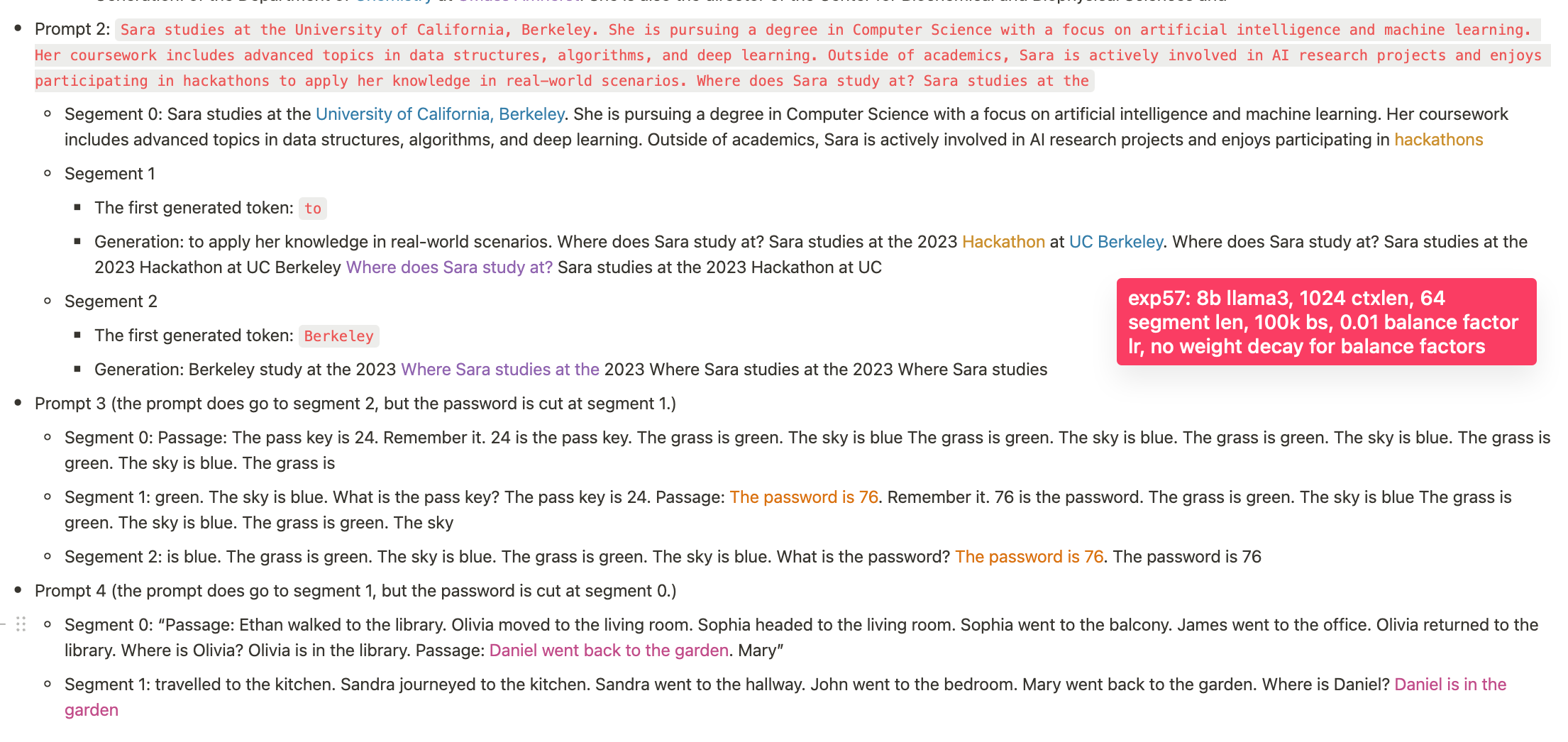
- 0-short: 在提示 2 中,模型能够回忆起一个人的学习地点 (昨天的 8b 模型未能做到这一点),但在信息点密钥测试中失败 (尚未全面运行; 将会进行)。
- 1-short
- 提示 3: 模型能够识别一个人的位置。
- 提示 4: 模型通过了信息点密钥测试
在这些情况下,模型能够继续生成早期片段的精确内容。(在我们之前的实验中,模型无法继续生成早期片段的精确内容,只能生成大致相关的内容; 因此新模型已经有了显著改进。)
第 6 节: 结论
遗憾的是,尽管取得了这些进展,我们发现在我们的实验中,Infini-attention 并不够令人信服,特别是在可靠性方面还不够。在我们复现的这个阶段,我们仍然认为 Ring Attention、YaRN 和 rope scaling 是将预训练模型扩展到更长上下文长度的更好选择。
这些后来的技术对于非常大的模型 (例如,400B 及以上) 仍然需要大量资源。因此,我们仍然认为探索压缩技术或继续推进我们在这篇博文中描述的一系列实验对社区来说具有重大意义,我们也很兴奋能够跟进并尝试可能开发出的新技术,来克服当前工作的一些局限性。
总结
- 训练神经网络的含义: 提供优质数据,设置架构和训练以接收良好的梯度信号,并允许其收敛。
- Infini-attention 的长上下文性能随着我们压缩记忆的次数增加而下降。
- 门控机制很重要; 调整训练以允许门控收敛可以改善 Infini-attention 的长上下文性能 (但还不够好)。
- 始终训练一个良好的参考模型作为基线来衡量进展。
- 还有另一个错误会扰乱注意力输出的维度,导致即使在整个训练过程中损失减少,模型仍然无法在其片段长度内生成连贯的文本。经验教训: 即使你对模型的条件设置不佳,梯度下降仍然可以找到减少损失的方法。然而,模型不会按预期工作,所以要始终进行评估。
致谢
感谢 Leandro von Werra 和 Thomas Wolf 对项目的指导,以及 Tsendsuren Munkhdalai 分享原始实验的额外细节。我们也感谢 Leandro 对博文的反馈,并感谢 Hugging Face 的科学集群提供的计算资源。
赞赏英文原文: https://hf.co/blog/infini-attention
原文作者: neuralink, Leandro von Werra, Thomas Wolf
译者: smartisan
 微信赞赏
微信赞赏 支付宝赞赏
支付宝赞赏

