基于 transformer 的编码器-解码器模型是 表征学习 和 模型架构 这两个领域多年研究成果的结晶。本文简要介绍了神经编码器-解码器模型的历史，更多背景知识，建议读者阅读由 Sebastion Ruder 撰写的这篇精彩 博文。此外，建议读者对 自注意力 (self-attention) 架构 有一个基本了解，可以阅读 Jay Alammar 的 这篇博文 复习一下原始 transformer 模型。
本文分 4 个部分:
- 背景 – 简要回顾了神经编码器-解码器模型的历史，重点关注基于 RNN 的模型。
- 编码器-解码器 – 阐述基于 transformer 的编码器-解码器模型，并阐述如何使用该模型进行推理。
- 编码器 – 阐述模型的编码器部分。
- 解码器 – 阐述模型的解码器部分。
每个部分都建立在前一部分的基础上，但也可以单独阅读。这篇分享是第二部分 编码器-解码器。
编码器-解码器
2017 年，Vaswani 等人引入了 transformer 架构，从而催生了 基于 transformer 的编码器-解码器模型。
与基于 RNN 的编码器-解码器模型类似，基于 transformer 的编码器-解码器模型由一个编码器和一个解码器组成，且其编码器和解码器均由 残差注意力模块 (residual attention blocks) 堆叠而成。基于 transformer 的编码器-解码器模型的关键创新在于: 残差注意力模块无需使用循环结构即可处理长度 $n$ 可变的输入序列 $\mathbf{X}_{1:n}$。不依赖循环结构使得基于 transformer 的编码器-解码器可以高度并行化，这使得模型在现代硬件上的计算效率比基于 RNN 的编码器-解码器模型高出几个数量级。
回忆一下，要解决 序列到序列 问题，我们需要找到输入序列 $\mathbf{X}{1:n}$ 到变长输出序列 $\mathbf{Y}{1:m}$ 的映射。我们看看如何使用基于 transformer 的编码器-解码器模型来找到这样的映射。
与基于 RNN 的编码器-解码器模型类似，基于 transformer 的编码器-解码器模型定义了在给定输入序列 $\mathbf{X}{1:n}$ 条件下目标序列 $\mathbf{Y}{1:m}$ 的条件分布:
$$
p{\theta{\text{enc}}, \theta{\text{dec}}}(\mathbf{Y}{1:m} | \mathbf{X}_{1:n})
$$
基于 transformer 的编码器部分将输入序列 $\mathbf{X}_{1:n}$ 编码为 隐含状态序列 $\mathbf{\overline{X}}_{1:n}$，即:
$$
f{\theta{\text{enc}}}: \mathbf{X}{1:n} \to \mathbf{\overline{X}}{1:n}
$$
然后，基于 transformer 的解码器负责建模在给定隐含状态序列 $\mathbf{\overline{X}}{1:n}$ 的条件下目标向量序列 $\mathbf{Y}{1:m}$ 的概率分布:
$$
p{\theta{dec}}(\mathbf{Y}{1:m} | \mathbf{\overline{X}}{1:n})$$
根据贝叶斯法则，该序列分布可被分解为每个目标向量 $\mathbf{y}i$ 在给定隐含状态 $\mathbf{\overline{X} }{1:n}$ 和其所有前驱目标向量 $\mathbf{Y}_{0:i-1}$ 时的条件概率之积:
$$
p{\theta{dec}}(\mathbf{Y}{1:m} | \mathbf{\overline{X}}{1:n}) = \prod{i=1}^{m} p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})
$$
因此，在生成 $\mathbf{y}i$ 时，基于 transformer 的解码器将隐含状态序列 $\mathbf{\overline{X}}{1:n}$ 及其所有前驱目标向量 $\mathbf{Y}_{0 :i-1}$ 映射到 logit 向量 $\mathbf{l}_i$。 然后经由 softmax 运算对 logit 向量 $\mathbf{l}i$ 进行处理，从而生成条件分布 $p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})$。这个流程跟基于 RNN 的解码器是一样的。然而，与基于 RNN 的解码器不同的是，在这里，目标向量 $\mathbf{y}_i$ 的分布是 显式 (或直接) 地以其所有前驱目标向量 $\mathbf{y}0, \ldots, \mathbf{y}{i-1}$ 为条件的，稍后我们将详细介绍。此处第 0 个目标向量 $\mathbf{y}0$ 仍表示为 $\text{BOS}$ 向量。有了条件分布 $p{\theta_{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X} }_{1:n})$，我们就可以 自回归 生成输出了。至此，我们定义了可用于推理的从输入序列 $\mathbf{X}{1:n}$ 到输出序列 $\mathbf{Y}{1:m}$ 的映射。
我们可视化一下使用 基于 transformer 的编码器-解码器模型 _自回归_地生成序列的完整过程。
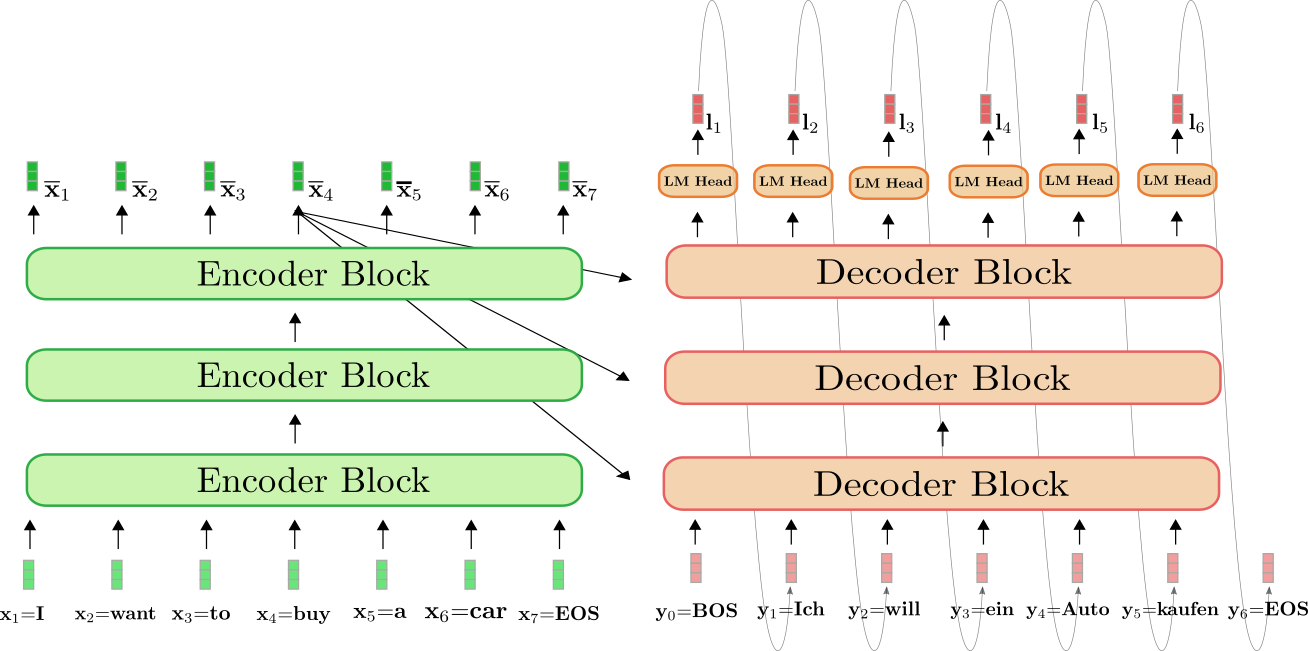
上图中，绿色为基于 transformer 的编码器，红色为基于 transformer 的解码器。与上一节一样，我们展示了如何将表示为 $(\mathbf{x}_1 = \text{I}，\mathbf{ x}_2 = \text{want}，\mathbf{x}_3 = \text{to}，\mathbf{x}_4 = \text{buy}，\mathbf{x}_5 = \text{a}，\mathbf{x}_6 = \text{car}，\mathbf{x}_7 = \text{EOS})$ 的英语句子 “I want to buy a car” 翻译成表示为 $(\mathbf{y}_0 = \text{BOS}，\mathbf{y }_1 = \text{Ich}，\mathbf{y}_2 = \text{will}，\mathbf{y}_3 = \text{ein}，\mathbf{y}_4 = \text{Auto}，\mathbf{y}_5 = \text{kaufen}，\mathbf{y}_6=\text{EOS})$ 的德语句子 “Ich will ein Auto kaufen”。
首先，编码器将完整的输入序列 $\mathbf{X}{1:7}$ = “I want to buy a car” (由浅绿色向量表示) 处理为上下文相关的编码序列 $\mathbf{\overline{X}}{1:7}$。这里上下文相关的意思是， 举个例子 ，$\mathbf{\overline{x}}_4$ 的编码不仅取决于输入 $\mathbf{x}_4$ = “buy”，还与所有其他词 “I”、“want”、“to”、“a”、“car” 及 “EOS” 相关，这些词即该词的 上下文 。
接下来，输入编码 $\mathbf{\overline{X}}_{1:7}$ 与 BOS 向量 ( 即 $\mathbf{y}0$) 被一起馈送到解码器。解码器将输入 $\mathbf{\overline{X}}{1:7}$ 和 $\mathbf{y}_0$ 变换为第一个 logit $\mathbf{l }_1$ (图中以深红色显示)，从而得到第一个目标向量 $\mathbf{y}_1$ 的条件分布:
$$
p{\theta{enc, dec}}(\mathbf{y} | \mathbf{y}0, \mathbf{X}{1:7}) = p{\theta{enc, dec}}(\mathbf{y} | \text{BOS}, \text{I want to buy a car EOS}) = p{\theta{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7})
$$
然后，从该分布中采样出第一个目标向量 $\mathbf{y}_1$ = $\text{Ich}$ (由灰色箭头表示)，得到第一个输出后，我们会并将其继续馈送到解码器。现在，解码器开始以 $\mathbf{y}_0$ = “BOS” 和 $\mathbf{y}_1$ = “Ich” 为条件来定义第二个目标向量的条件分布 $\mathbf{y}_2$:
$$
p{\theta{dec}}(\mathbf{y} | \text{BOS Ich}, \mathbf{\overline{X}}_{1:7})
$$
再采样一次，生成目标向量 $\mathbf{y}_2$ = “will”。重复该自回归过程，直到第 6 步从条件分布中采样到 EOS:
$$
\text{EOS} \sim p{\theta{dec}}(\mathbf{y} | \text{BOS Ich will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7})
$$
这里有一点比较重要，我们仅在第一次前向传播时用编码器将 $\mathbf{X}{1:n}$ 映射到 $\mathbf{\overline{X}}{1:n}$。从第二次前向传播开始，解码器可以直接使用之前算得的编码 $\mathbf{\overline{X}}_{1:n}$。为清楚起见，下图画出了上例中第一次和第二次前向传播所需要做的操作。
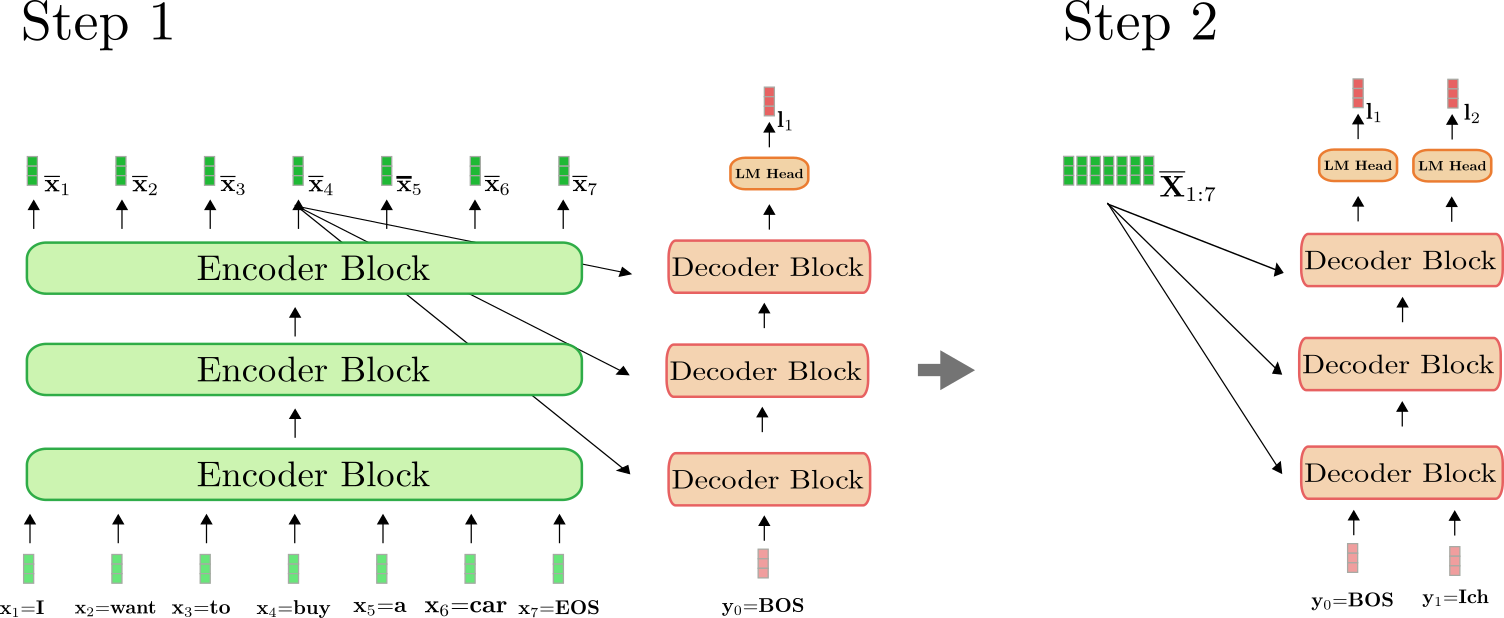
可以看出，仅在步骤 $i=1$ 时，我们才需要将 “I want to buy a car EOS” 编码为 $\mathbf{\overline{X}}_{1:7}$。从 $i=2$ 开始，解码器只是简单地复用了已生成的编码。
在 🤗 transformers 库中，这一自回归生成过程是在调用 .generate() 方法时在后台完成的。我们用一个翻译模型来实际体验一下。
from transformers import MarianMTModel, MarianTokenizer
tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids
# translate example
output_ids = model.generate(input_ids)[0]
# decode and print
print(tokenizer.decode(output_ids))输出:
<pad> Ich will ein Auto kaufen.generate() 接口做了很多事情。首先，它将 input_ids 传递给编码器。然后，它将一个预定义的标记连同已编码的 input_ids 一起传递给解码器 (在使用 MarianMTModel 的情况下，该预定义标记为 $\text{<pad>}$ )。接着，它使用波束搜索解码机制根据最新的解码器输出的概率分布 ${}^1$ 自回归地采样下一个输出词。更多有关波束搜索解码工作原理的详细信息，建议阅读 这篇博文。
我们在附录中加入了一个代码片段，展示了如何“从头开始”实现一个简单的生成方法。如果你想要完全了解 自回归 生成的幕后工作原理，强烈建议阅读附录。
总结一下:
- 基于 transformer 的编码器实现了从输入序列 $\mathbf{X}{1:n}$ 到上下文相关的编码序列 $\mathbf{\overline{X}}{1 :n}$ 之间的映射。
- 基于 transformer 的解码器定义了条件分布 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{ \overline{X}}_{1:n})$。
- 给定适当的解码机制，可以自回归地从 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}{1:n}), \forall i \in {1, \ldots, m}$ 中采样出输出序列 $\mathbf{Y}{1:m}$。
太好了，现在我们已经大致了解了 基于 transformer 的 编码器-解码器模型的工作原理。下面的部分，我们将更深入地研究模型的编码器和解码器部分。更具体地说，我们将确切地看到编码器如何利用自注意力层来产生一系列上下文相关的向量编码，以及自注意力层如何实现高效并行化。然后，我们将详细解释自注意力层在解码器模型中的工作原理，以及解码器如何通过 交叉注意力 层以编码器输出为条件来定义分布 $p{\theta{\text{dec}}}(\mathbf{y}i | \mathbf{Y}{0: i-1}, \mathbf{\overline{X}}_{1:n})$。在此过程中，基于 transformer 的编码器-解码器模型如何解决基于 RNN 的编码器-解码器模型的长程依赖问题的答案将变得显而易见。
${}^1$ 可以从 此处 获取 "Helsinki-NLP/opus-mt-en-de" 的解码参数。可以看到，其使用了 num_beams=6 的波束搜索。
敬请关注其余部分的文章。
赞赏英文原文: https://hf.co/blog/encoder-decoder
原文作者: Patrick von Platen
译者: Matrix Yao (姚伟峰)，英特尔深度学习工程师，工作方向为 transformer-family 模型在各模态数据上的应用及大规模模型的训练推理。
审校/排版: zhongdongy (阿东)
微信赞赏
支付宝赞赏
相关文章
